こんにちは、ケイです。
今回は受験で頻出の用語、”偏差値“について解説をしていきます。
高校生なら、模試や定期テストの結果が返ってきたときに必ず目にしますよね。
友達同士の会話、先生との会話、気軽に”偏差値”ってワードを使っていると思います。
しかし、
偏差値ってぶっちゃけ、どういう数値なのか、きちんと解説できますか?
こういわれると、受験生ですら、「No」の人が大半だと思います。
偏差値を理解するには、数Bの、「確率分布と統計的な推測」の単元を学習している必要がありますが、
この単元をやらない高校も多いため、偏差値がどういう数値なのか、分からなくても当然です。
この記事では、偏差値について、「確率分布と統計的な推測」の単元を学習していない人にも分かるよう、解説していきます。
では本題に入ります。最後まで読んでいってくださいね!
偏差値の求め方
偏差値の公式
偏差値の公式については、軽く目を通していただくだけで問題ありません。
偏差値の公式は、以下の通りとなります。
$$\frac{10 × (自分の点数-全体の平均点)}{標準偏差} + 50$$
また、標準偏差は、
n人のそれぞれの点数を $x_1,x_2,…x_n$ 、n人の平均点を$x_a$とすると、
$$\sqrt{\frac{(x_1-x_a)^2+(x_2-x_a)^2…(x_n-x_a)^2}{n}}$$
以上のような計算を経て、偏差値を計算しています。
思っているより複雑な計算式で、特に標準偏差の計算が、非常に手間のかかる計算であることがわかると思います!
偏差値の意味について
偏差値の意味合いとしては、一言で説明すると、
もし点数の分布が、正規分布に近い形で分布していると仮定したときに、
平均を50として、どれだけ離れているのかを表した指標
このように表すことができます。
上の文の中で、正規分布、これはあまり聞いたことがないかな、と思います。
正規分布は、偏差値がどういう数値であるかを理解するのに必要なキーワードとなりますので、解説していきます。
次の見出しである、”正規分布について” は、少々難しい話になりますが、「こんな考え方があるんだ」程度で見ておいてください。
正規分布について
正規分布とは、統計学で用いられる、データの分布図のことで、以下の式
$標準偏差を \sigma ,データの平均値を \mu としたとき、$
$$f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$$
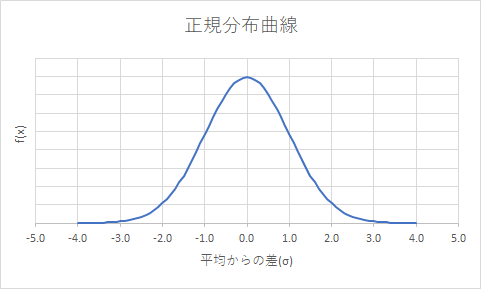
この式で描かれるグラフのことを正規分布曲線といい、
データ全体が正規分布曲線にしたがって分布することを、正規分布をとるいいます。
この正規分布は、統計学の分野において、
データを取って、もしそれが理想的に分布した場合、どのようにデータが分布し、散らばっていくのか、
というモデルとして扱われています。
上記の式で描かれる、正規分布曲線は、下の画像のようになります。
データの分布が、正規分布に近い形で分布している、とは?
少し難しい話をしましたが、ここからは、偏差値の場合について考えてみます。
先ほどの正規分布曲線を、偏差値の場合に置き換えてみると、以下の画像のようになります。
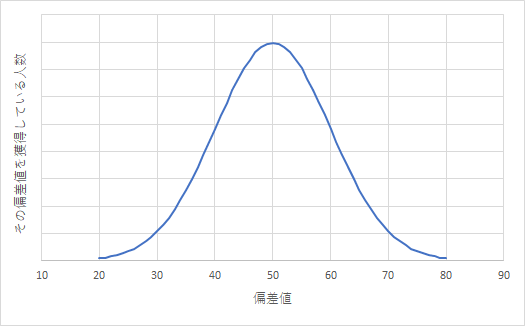
偏差値の意味合いを一言で説明した部分を再掲します。
もし点数の分布が、正規分布に近い形で分布していると仮定したときに、
平均を50として、どれだけ離れているのかを表した指標
つまり、点数の分布が、正規分布に近い形で分布していると仮定、の意味は、
偏差値を計算する上では、上記の曲線のように点数が分布している、と想定していますよ、
ということになります。
偏差値が意味のない数値になる場合とは?
先ほども言った通り、偏差値を計算する上では、正規曲線のように点数が分布している、ということを想定しています。
例を一つ挙げましょう。
例えば、これは極端ですが、点数の分布がこのようになっている場合はどうでしょう?
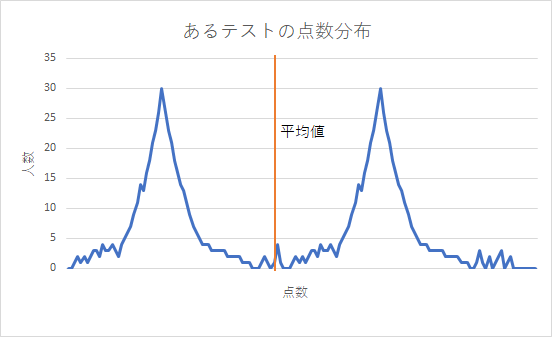
これは、山が2つできてしまっていて、下の画像と比べても、似ても似つかない形になっていますね。
特に、偏差値の計算では、偏差値50、つまり平均が最も人数が多い(最頻値)と想定しているのに、
上の画像では、平均は山と山の間の、人数が少ない部分となってしまっています。

このような極端な点数分布となってしまった場合、偏差値は意味をなさない数値となってしまいます。
偏差値が意味のある数字なのかどうかは、
テストや模試の、全受験者の点数分布表を確認して、判断するようにしてくださいね!
同じ大学の同じ学部・学科でも、会社によって偏差値が違うのはどうして?
例えば、日本の最高峰である、東京大学理科三類の偏差値を見てみましょう。
ベネッセ 81
河合塾 72.5
東進 76
このように、会社によって偏差値の数値が変わっています。
これは、それぞれの模試を受ける人が違うからです。
例えば、ベネッセ模試のように、上位層から下位層まで幅広く受ける模試の場合は、上位層と下位層の差も大きくなってしまいます。
このため、偏差値が大きく算出される傾向にあります。
ここには駿台の偏差値は非公開となっており、ありませんが、
駿台全国模試のように、国公立大学~東大・京大を目指す人、つまり学力上位層ばかりが受ける模試では、
学力差は小さくなるため、上位層と下位層の差は小さくなります。
このため、偏差値は小さく算出される傾向にあります。
また、会社により、偏差値の算出の方法も異なっており、
会社間で偏差値を比べる、というのは意味がないです。
模試の偏差値が下がっちゃった。。これって学力が下がったの?
模試を何度も受けていくと、偏差値が上下することもあると思います。
上がったときは嬉しいけど、下がるとやっぱり心配ですよね。
しかし、偏差値は、模試を受ける人が違うと、偏差値も変わってくるものです。
学校の定期テストであれば、受ける人は同じなので、偏差値の上下は重要ですが、
模試は、たとえ同じ会社の模試であっても、回によって受ける人は変わってきます。
模試の偏差値の上下はあまり気にせずに、間違えてしまった問題を復習していって、
学力を伸ばしていきましょう!
偏差値○○の人は上位何パーセントなの?
これに関しては、まず大前提として、
点数の分布が、正規分布に近い形で分布している
この条件においての数値であることを理解しておいてください。
点数分布が正規分布に近い形で分布している時の、
偏差値が○○であるとき、上位何パーセントかの表を、下に掲載します。
| 偏差値 | 上位何%か | 偏差値 | 上位何%か | 偏差値 | 上位何%か | 偏差値 | 上位何%か |
| 50 | 50.0% | 60 | 15.9% | 70 | 2.28% | 80 | 0.13% |
| 51 | 46.0% | 61 | 13.6% | 71 | 1.79% | 81 | 0.10% |
| 52 | 42.1% | 62 | 11.5% | 72 | 1.39% | 82 | 0.07% |
| 53 | 38.2% | 63 | 9.68% | 73 | 1.07% | 83 | 0.05% |
| 54 | 34.5% | 64 | 8.08% | 74 | 0.82% | 84 | 0.03% |
| 55 | 30.9% | 65 | 6.68% | 75 | 0.62% | 85 | 0.02% |
| 56 | 27.4% | 66 | 5.48% | 76 | 0.47% | ||
| 57 | 24.2% | 67 | 4.46% | 77 | 0.35% | ||
| 58 | 21.2% | 68 | 3.59% | 78 | 0.26% | ||
| 59 | 18.4% | 69 | 2.87% | 79 | 0.19% |
このようになっています。
偏差値55,60,65,70の人は、それぞれ上位30.9%、15.9%、6.68%、2.28%となることが分かります。
例を一つ上げると、100,000人が受けた模試で、
- 偏差値50→約50,000位/100,000人中
- 偏差値55→ 約30,900位/100,000人中
- 偏差値60→約15,900位/100,000人中
- 偏差値65→ 約6,680位/100,000人中
- 偏差値70→ 約2,280位/100,000人中
ということになります。
こう見ると、同じ、偏差値10上げるでも、
50→60の人と、60→70の人では、60→70の方が比べ物にならないほど大変で、努力が必要であることがわかりますね。
まとめ
偏差値は、あくまでも自分が全体から見て、どの位置にいるかを示すだけの指標です。
偏差値を正しく理解して、偏差値に振り回されることなく、
学力を向上していけることを応援しています。
この記事を読んで、偏差値とうまく付き合っていけるようになったら幸いです。
本記事はこれでおしまいです。
ここまで読んでいただき、ありがとうございました!




コメント